线性回归代码实现

在了解了线性回归的背景知识之后，现在我们可以动手实现它了。尽管强大的深度学习框架可以减少大量重复性工作，但若过于依赖它提供的便利，会导致我们很难深入理解深度学习是如何工作的。因此，本节将介绍如何只利用Tensor和GradientTape来实现一个线性回归的训练。

首先，导入本节中实验所需的包或模块，其中的matplotlib包可用于作图，且设置成嵌入显示。

%matplotlib inline
import tensorflow as tf
print(tf.__version__)
from matplotlib import pyplot as plt
import random

    2.0.0

手动实现

生成数据集

我们构造一个简单的人工训练数据集，它可以使我们能够直观比较学到的参数和真实的模型参数的区别。设训练数据集样本数为1000，输入个数（特征数）为2。给定随机生成的批量样本特征 $\boldsymbol{X} \in \mathbb{R}^{1000 \times 2}$，我们使用线性回归模型真实权重 $\boldsymbol{w} = [2, -3.4]^\top$ 和偏差 $b = 4.2$，以及一个随机噪声项 $\epsilon$ 来生成标签

$$\boldsymbol{y} = \boldsymbol{X}\boldsymbol{w} + b + \epsilon$$

其中噪声项 $\epsilon$ 服从均值为0、标准差为0.01的正态分布。噪声代表了数据集中无意义的干扰。下面，让我们生成数据集。

num_inputs = 2
num_examples = 1000
true_w = [2, -3.4]
true_b = 4.2
features = tf.random.normal((num_examples, num_inputs),stddev = 1)
labels = true_w[0] * features[:,0] + true_w[1] * features[:,1] + true_b
labels += tf.random.normal(labels.shape,stddev=0.01)

注意，features的每一行是一个长度为2的向量，而labels的每一行是一个长度为1的向量（标量）。

print(features[0], labels[0])

输出：

(<tf.Tensor: id=31, shape=(2,), dtype=float32, numpy=array([0.24220389, 0.41220406], dtype=float32)>,
 <tf.Tensor: id=35, shape=(), dtype=float32, numpy=3.3064191>)

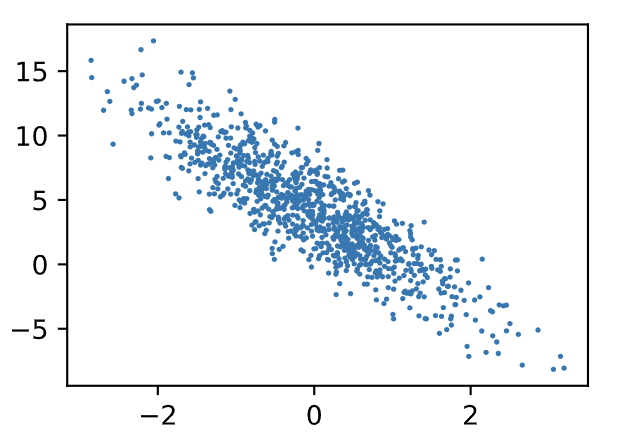
通过生成第二个特征features[:, 1]和标签 labels 的散点图，可以更直观地观察两者间的线性关系。

def set_figsize(figsize=(3.5, 2.5)):
    plt.rcParams['figure.figsize'] = figsize

set_figsize()
plt.scatter(features[:, 1], labels, 1)

读取数据

在训练模型的时候，我们需要遍历数据集并不断读取小批量数据样本。这里我们定义一个函数：它每次返回batch_size（批量大小）个随机样本的特征和标签。

def data_iter(batch_size, features, labels):
    num_examples = len(features)
    indices = list(range(num_examples))
    random.shuffle(indices)
    for i in range(0, num_examples, batch_size):
        j = indices[i: min(i+batch_size, num_examples)]
        yield tf.gather(features, axis=0, indices=j), tf.gather(labels, axis=0, indices=j)

让我们读取第一个小批量数据样本并打印。每个批量的特征形状为(10, 2)，分别对应批量大小和输入个数；标签形状为批量大小。

batch_size = 10

for X, y in data_iter(batch_size, features, labels):
    print(X, y)
    break

输出：

tf.Tensor(
[[ 0.04718596 -1.5959413 ]
 [ 0.3889716  -1.5288432 ]
 [-1.8489572   1.66422   ]
 [-1.3978077  -0.85818154]
 [-0.36940867 -0.619267  ]
 [-0.15660426  1.1231796 ]
 [ 0.89411694  1.5499148 ]
 [ 1.9971682  -0.56981105]
 [-2.1852891   0.18805206]
 [ 1.3222371  -1.0301086 ]], shape=(10, 2), dtype=float32) tf.Tensor(
[ 9.738684   10.164594   -5.15065     4.3305573   5.568048    0.06494669
  0.7251317  10.128626   -0.8036391  10.343082  ], shape=(10,), dtype=float32)

初始化模型参数

我们将权重初始化成均值为0、标准差为0.01的正态随机数，偏差则初始化成0。

w = tf.Variable(tf.random.normal((num_inputs, 1), stddev=0.01))
b = tf.Variable(tf.zeros((1,)))

定义模型

下面是线性回归的矢量计算表达式的实现。我们使用matmul函数做矩阵乘法。

def linreg(X, w, b):
    return tf.matmul(X, w) + b

定义损失函数

我们使用上一节描述的平方损失来定义线性回归的损失函数。在实现中，我们需要把真实值y变形成预测值y_hat的形状。以下函数返回的结果也将和y_hat的形状相同。

def squared_loss(y_hat, y):
    return (y_hat - tf.reshape(y, y_hat.shape)) ** 2 /2

定义优化算法

以下的sgd函数实现了上一节中介绍的小批量随机梯度下降算法。它通过不断迭代模型参数来优化损失函数。这里自动求梯度模块计算得来的梯度是一个批量样本的梯度和。我们将它除以批量大小来得到平均值。

def sgd(params, lr, batch_size, grads):
    """Mini-batch stochastic gradient descent."""
    for i, param in enumerate(params):
        param.assign_sub(lr * grads[i] / batch_size)

训练模型

在训练中，我们将多次迭代模型参数。在每次迭代中，我们根据当前读取的小批量数据样本（特征X和标签y），通过调用反向函数t.gradients计算小批量随机梯度，并调用优化算法sgd迭代模型参数。由于我们之前设批量大小batch_size为10，每个小批量的损失l的形状为(10, 1)。回忆一下自动求梯度一节。由于变量l并不是一个标量，所以我们可以调用reduce_sum()将其求和得到一个标量，再运行t.gradients得到该变量有关模型参数的梯度。注意在每次更新完参数后不要忘了将参数的梯度清零。

在一个迭代周期（epoch）中，我们将完整遍历一遍data_iter函数，并对训练数据集中所有样本都使用一次（假设样本数能够被批量大小整除）。这里的迭代周期个数num_epochs和学习率lr都是超参数，分别设3和0.03。在实践中，大多超参数都需要通过反复试错来不断调节。虽然迭代周期数设得越大模型可能越有效，但是训练时间可能过长。而有关学习率对模型的影响，我们会在后面“优化算法”一章中详细介绍。

lr = 0.03
num_epochs = 3
net = linreg
loss = squared_loss

for epoch in range(num_epochs):
    for X, y in data_iter(batch_size, features, labels):
        with tf.GradientTape() as t:
            t.watch([w,b])
            l = tf.reduce_sum(loss(net(X, w, b), y))
        grads = t.gradient(l, [w, b])
        sgd([w, b], lr, batch_size, grads)
    train_l = loss(net(features, w, b), labels)
    print('epoch %d, loss %f' % (epoch + 1, tf.reduce_mean(train_l)))

输出：

 epoch 1, loss 0.028907 epoch 2, loss 0.000101 epoch 3, loss 0.000049

训练完成后，我们可以比较学到的参数和用来生成训练集的真实参数。它们应该很接近。

print(true_w, w)
print(true_b, b)

输出：

([2, -3.4], <tf.Variable 'Variable:0' shape=(2, 1) dtype=float32, numpy= array([[ 1.9994558], [-3.3993363]], dtype=float32)>) (4.2, <tf.Variable 'Variable:0' shape=(1,) dtype=float32, numpy=array([4.199041], dtype=float32)>)

使用框架实现

随着深度学习框架的发展，开发深度学习应用变得越来越便利。实践中，我们通常可以用比上一节更简洁的代码来实现同样的模型。在本节中，我们将介绍如何使用tensorflow2.0推荐的keras接口更方便地实现线性回归的训练。

生成数据集

我们生成与上一节中相同的数据集。其中features是训练数据特征，labels是标签。

import tensorflow as tf

num_inputs = 2
num_examples = 1000
true_w = [2, -3.4]
true_b = 4.2
features = tf.random.normal(shape=(num_examples, num_inputs), stddev=1)
labels = true_w[0] * features[:, 0] + true_w[1] * features[:, 1] + true_b
labels += tf.random.normal(labels.shape, stddev=0.01)

读取数据

虽然tensorflow2.0对于线性回归可以直接拟合，不用再划分数据集，但我们仍学习一下读取数据的方法

from tensorflow import data as tfdata

batch_size = 10
# 将训练数据的特征和标签组合
dataset = tfdata.Dataset.from_tensor_slices((features, labels))
# 随机读取小批量
dataset = dataset.shuffle(buffer_size=num_examples) 
dataset = dataset.batch(batch_size)
data_iter = iter(dataset)

shuffle 的 buffer_size 参数应大于等于样本数，batch 可以指定 batch_size 的分割大小。

for X, y in data_iter:
    print(X, y)
    break

tf.Tensor(
[[ 1.2856768   1.3815335 ]
 [ 1.1151928  -1.3777982 ]
 [ 0.6097271   1.3478378 ]
 [ 2.1615875   1.52963   ]
 [-1.3143488  -0.79531455]
 [-2.495006    0.3701927 ]
 [-0.07739297 -0.8636043 ]
 [-0.18479416 -1.5275241 ]
 [-0.3426277  -0.01935842]
 [ 0.25231913  1.4940815 ]], shape=(10, 2), dtype=float32) tf.Tensor(
[ 2.0673854  11.10116     0.8320709   3.3300133   4.272185   -2.062947
  6.981174    9.027803    3.5848885  -0.39152586], shape=(10,),     dtype=float32)

使用iter(dataset)的方式，只能遍历数据集一次，是一种比较 tricky 的写法，为了复刻原书表达才这样写。这里也给出一种在官方文档中推荐的写法：

for (batch, (X, y)) in enumerate(dataset):
    print(X, y)
    break

定义模型和初始化参数

Tensorflow 2.0推荐使用Keras定义网络，故使用Keras定义网络。我们先定义一个模型变量model，它是一个Sequential实例。在Keras中，Sequential实例可以看作是一个串联各个层的容器。在构造模型时，我们在该容器中依次添加层。当给定输入数据时，容器中的每一层将依次推断下一层的输入尺寸。重要的一点是，在Keras中我们无须指定每一层输入的形状。线性回归，输入层与输出层等效为一层全连接层keras.layers.Dense()。

Keras 中初始化参数由 kernel_initializer 和 bias_initializer 选项分别设置权重和偏置的初始化方式。我们从 tensorflow 导入 initializers 模块，指定权重参数每个元素将在初始化时随机采样于均值为0、标准差为0.01的正态分布。偏差参数默认会初始化为零。RandomNormal(stddev=0.01)指定权重参数每个元素将在初始化时随机采样于均值为0、标准差为0.01的正态分布。偏差参数默认会初始化为零。

from tensorflow import keras
from tensorflow.keras import layers
from tensorflow import initializers as init
model = keras.Sequential()
model.add(layers.Dense(1, kernel_initializer=init.RandomNormal(stddev=0.01)))

定义损失函数

Tensoflow在losses模块中提供了各种损失函数和自定义损失函数的基类，并直接使用它的均方误差损失作为模型的损失函数。

from tensorflow import losses
loss = losses.MeanSquaredError()

定义优化算法

同样，我们也无须自己实现小批量随机梯度下降算法。tensorflow.keras.optimizers 模块提供了很多常用的优化算法比如SGD、Adam和RMSProp等。下面我们创建一个用于优化model 所有参数的优化器实例，并指定学习率为0.03的小批量随机梯度下降（SGD）为优化算法。

from tensorflow.keras import optimizers
trainer = optimizers.SGD(learning_rate=0.03)

训练模型

在使用Tensorflow训练模型时，我们通过调用tensorflow.GradientTape记录动态图梯度，执行tape.gradient获得动态图中各变量梯度。通过 model.trainable_variables 找到需要更新的变量，并用 trainer.apply_gradients 更新权重，完成一步训练。

num_epochs = 3
for epoch in range(1, num_epochs + 1):
    for (batch, (X, y)) in enumerate(dataset):
        with tf.GradientTape() as tape:
            l = loss(model(X, training=True), y)
        
        grads = tape.gradient(l, model.trainable_variables)
        trainer.apply_gradients(zip(grads, model.trainable_variables))
    
    l = loss(model(features), labels)
    print('epoch %d, loss: %f' % (epoch, l))

epoch 1, loss: 0.519287
epoch 2, loss: 0.008997
epoch 3, loss: 0.000261

下面我们分别比较学到的模型参数和真实的模型参数。我们可以通过model的get_weights()来获得其权重（weight）和偏差（bias）。学到的参数和真实的参数很接近。

true_w, model.get_weights()[0]

([2, -3.4], array([[ 1.9930198],
    [-3.3977082]], dtype=float32))

true_b, model.get_weights()[1]

(4.2, array([4.1895046], dtype=float32))